Online Spanner

logo

Online Spanner in metrischen Räumen

Leo Decking, 17.03.2022

This presentation was given in German, but it includes interactive implementations for different kinds of spanners. Give it a try :)

Über mich:

logo Leo Decking

21 Jahre
Paderborn
1. Semester Informatik
Nebenfach Musik

logo

Online Spanner in metrischen Räumen

Was soll das denn sein?🤔

Online Spanner in metrischen Räumen

$\text{Menge } X \text{ mit Abbildung } d: X\times X\rightarrow \mathbb{R}\\ \text{Für alle } x,y,z\in X \text{ gilt}:\\ \quad\\ \qquad d(x,y)\geq 0 \quad \text{ und } \quad d(x,y)=0 \Leftrightarrow x=y\\ d(x,y)=d(y,x)\\ d(x,z)\leq d(x,y)+d(y,z)$

In diesem Vortrag: Euklidischer Raum bzw. Ebene

Online Spanner in metrischen Räumen

$\text{Graph } G=(V,E) \text{ ist ein }\textbf{$t$-Spanner},\\ \text{wenn die Kanten E so gewählt sind, dass}\\ d_G(x,y) \leq t\cdot d(x,y) \quad\forall x,y\in V.\\ \quad\\ d_G(x,y) \text{ ist die Länge eines kürzesten Pfades in } G.\\ \quad\\ \text{Oft $t=1+\varepsilon$ mit $\varepsilon\in (0,1)$}\\$ $\textbf{Sparsity:}\quad\frac{\vert E\vert}{\vert E_{MST}\vert}\approx \frac{\vert E\vert}{\vert V\vert}\\ \textbf{Lightness:}\quad\frac{w(G)}{w(MST)}$

Online Spanner in metrischen Räumen

$\text{Punkte werden nacheinander bekannt gegeben.}\\ \text{In jedem Schritt muss $t$-Spanner erhalten bleiben.}\\ \Rightarrow \text{Kanten hinzufügen, aber keine entfernen}\\$ $\textbf{Competitive Ratio:}\\ \quad\sup_\sigma\frac{w_{ALG}(\sigma)}{w_{OPT}(\sigma)} \leq \sup_\sigma\frac{w_{ALG}(\sigma)}{w_{MST}(\sigma)}$

Online Greedy-Spanner

$\text{Graph } G=(V,E) \text{ ist ein }\textbf{$t$-Spanner},\\ \text{wenn die Kanten E so gewählt sind, dass}\\ d_G(x,y) \leq t\cdot d(x,y) \quad\forall x,y\in V.\\ \quad\\ \text{Für neuen Punkt }a:\\ 1. \text{ Sortiere Knoten $b\in V$ aufsteigend nach $d(a,b)$ }\\ 2. \text{ Für jeden Knoten $b\in V$: }\\ 2.1 \text{ Wenn $d_G(a,b)>t\cdot d(a,b)$, füge $(a,b)$ hinzu} \\$ $\text{Vorteile: }\\ \text{+ einfach zu verstehen }\\ \text{+ nur wenige Kanten }\\ \quad\\ \text{Nachteile: }\\ \text{- kürzeste Pfade müssen berechnet werden }$

Yao-Graphen

$\text{Graph } G=(V,E) \text{ ist ein }\textbf{$t$-Spanner},\\ \text{wenn die Kanten E so gewählt sind, dass}\\ d_G(x,y) \leq t\cdot d(x,y) \quad\forall x,y\in V.\\ \quad\\ \text{Für neuen Punkt }a:\\ 1. \text{ Stelle $\left\lceil\frac{2\pi}{2\sin^{-1}\left(\frac{1}{2}\left(1-\frac{1}{t}\right)\right)}\right\rceil$ Kegel um $a$ auf}\\ 2. \text{ Für jeden Kegel $C_i$: }\\ 2.1 \text{ Füge $(a,b)$ mit $b\in C_i$: $d(a,b)$ minimal hinzu} \\$

GeoGebra

$\text{Vorteile: }\\ \text{+ schnell zu berechnen }\\ \text{+ nur wenige Kanten }\\$

Yao-Graphen

$\text{Graph } G=(V,E) \text{ ist ein }\textbf{$t$-Spanner},\\ \text{wenn die Kanten E so gewählt sind, dass}\\ d_G(x,y) \leq t\cdot d(x,y) \quad\forall x,y\in V.\\ \quad\\ \text{Für neuen Punkt }a:\\ 1. \text{ Stelle $\left\lceil\frac{2\pi}{2\sin^{-1}\left(\frac{1}{2}\left(1-\frac{1}{t}\right)\right)}\right\rceil$ Kegel um $a$ auf}\\ 2. \text{ Für jeden Kegel $C_i$: }\\ 2.1 \text{ Füge $(a,b)$ mit $b\in C_i$: $d(a,b)$ minimal hinzu} \\$

GeoGebra

$\text{Vorteile: }\\ \text{+ schnell zu berechnen }\\ \text{+ nur wenige Kanten }\\ \quad\\ \text{Nachteile: }\\ \text{- viele lange Kanten möglich}\\ \text{- WorstCase: $\frac{w(G)}{w(MST)}=\mathcal{O}(n)$}$

Well Seperated Pair Decomposition

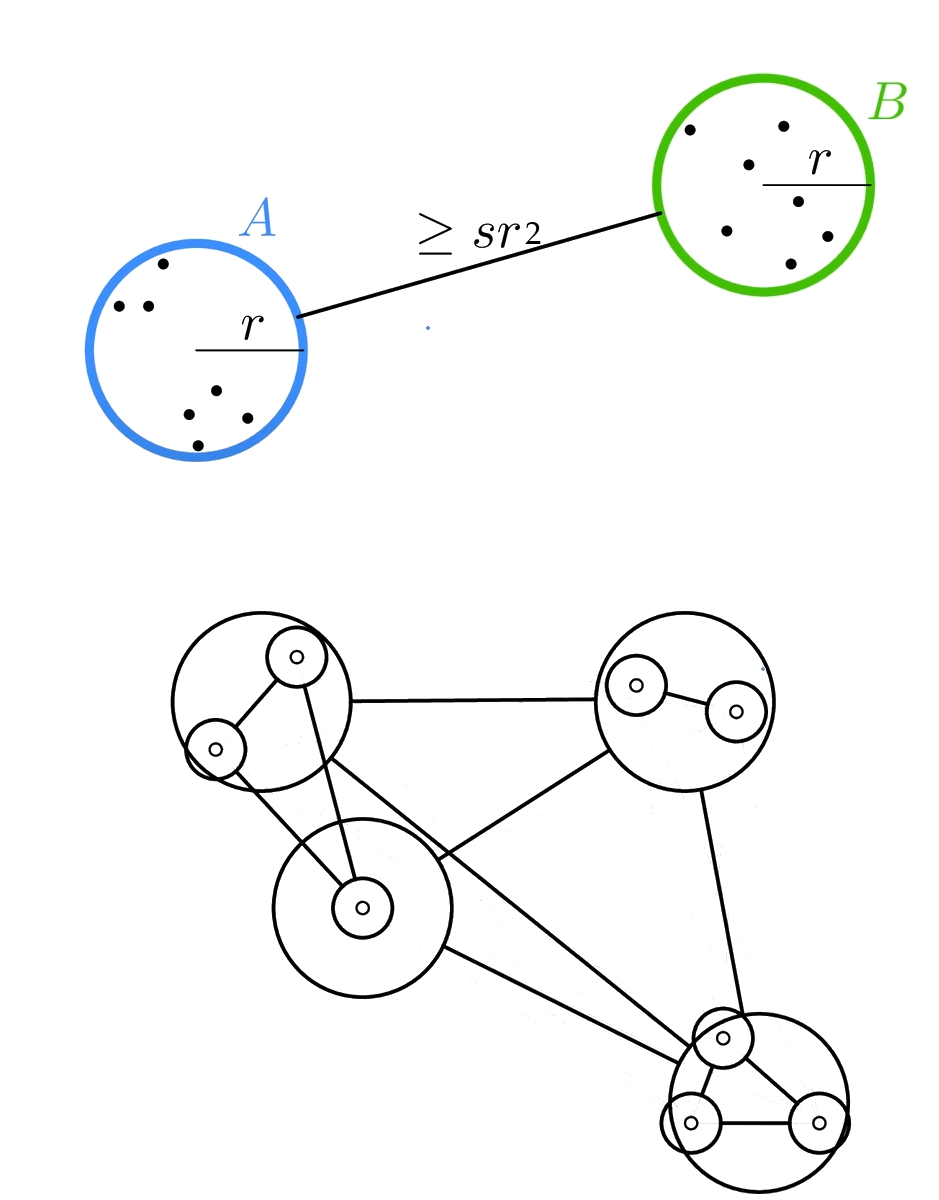
$\text{Knoten werden in $s$-well seperated pairs eingeteilt: }\\ s\cdot d(a_1,b_1) \geq d(a_2,a_3) \quad \forall a_i\in A, b_i\in B\\ \quad\\ \text{Für alle } (x,y)\in V\times V \text{ muss ein Paar $(A,B)$}\\ \text{existieren mit $x\in A, y\in B$.} \quad\\$ $\text{Um nun einen $t$-Spanner zu erhalten: }\\ \text{Setze } s=4+\frac{8}{t}.\\ \text{Für jedes Paar füge verbindene Kante hinzu.}$

Wie konstruiert man eine WSPD?

Quadtrees

Baumstruktur
Zellen werden viergeteilt bis jeder Knoten eigene Zelle hat

Jede Zelle $z$ hat Repräsentanten $r_z$

Compressed Quadtree

Ebenen können übersprungen werden
Sonst unendlich viele Ebenen möglich

Well Seperated Pair Decomposition

Baumstruktur
Zellen werden viergeteilt bis jeder Knoten eigene Zelle hat

Jede Zelle hat Repräsentanten

Compressed Quadtree

Level können übersprungen werden
Sonst unendlich viele Level möglich

Für neuen Knoten $r_p$ um WSPD zu erhalten:

Erstelle Paar mit Zellen $r_z$ auf höchstem Level
mit $d(r_p,r_z) \geq s\cdot $ø
Kanten $(r_p,r_z)$ hinzufügen

Nur wenn Elternteil jeweils noch nicht in einem Paar
Also $s\cdot $ ø $ \leq d(r_p,r_z) < s\cdot 2$ ø $
ø $:=0$, falls keine Kinder
$\Rightarrow$ Jeder andere Punkt landet in genau einem Paar

Kombinierter Spanner

Erhalte Quadtree

Auf jedem Level Yao-Graph der Repräsentanten

$\sqrt{t}$-Spanner, wenn im Quadtree alle Kanten
$(r_a,r_b)$ sind mit $s\cdot $ ø $ \leq d(r_a,r_b) < s\cdot 2$ ø

Jede Kante $(r_a,r_b)$ wäre in einem festen Level

Bestimmt durch ø

Im Yao-Graph des Levels gibt es Pfad mit Länge
$\sqrt{t}\cdot d(r_a,r_b) \leq \sqrt{t}\cdot s\cdot 2$ ø

Fazit

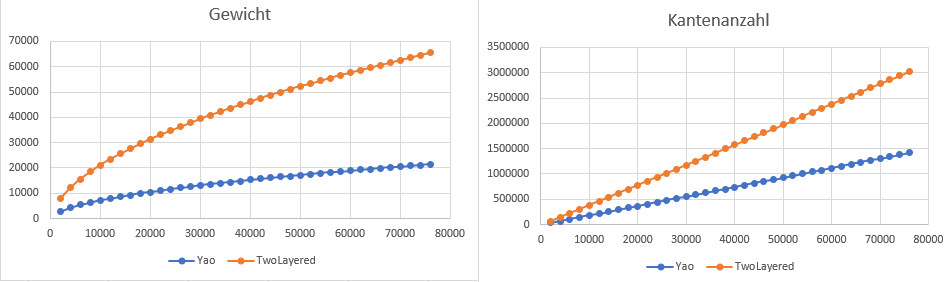Wir haben verschiedene Arten von Online Spannern in euklidischen Räumen kennengelernt, die jeweils Vor- und Nachteile haben.

Im durchschnittlichen Fall eignen sich Yao-Graphen am besten; der Greedy-Spanner wenn man nicht auf Ressourcen achten muss.
Ist der Greedy-Spanner im euklidischen Raum eventuell sogar optimal?

Quellen

Sujoy Bhore Arnold Filtser Hadi Khodabandeh Csaba D. Tóth: 'Online Spanners in Metric Spaces', 2022
Sariel Har-Peled: 'Geometric Approximation Algorithms', volume 173 of Mathematical Surveys and Monographs, 2011
Kevin Buchin: 'Well-separated pair decomposition and Spanners' https://youtu.be/L0m3jOwR-Aw
Andrew C. Yao: 'On Constructing Minimum Spanning Trees in k-Dimensional Spaces and Related Problems'. STAN-CS-77-642, 1977
Prosenjit Bose, Joachim Gudmundsson, and Pat Morin: 'Ordered theta graphs'. Computational Geometry, 28(1):11–18, 2004

Online Spanner in metrischen Räumen

Über mich:

Online Spanner in metrischen Räumen

Online Spanner in metrischen Räumen

Online Spanner in metrischen Räumen

Online Spanner in metrischen Räumen

Online Greedy-Spanner

Yao-Graphen

Yao-Graphen

Well Seperated Pair Decomposition

Quadtrees

Well Seperated Pair Decomposition

Kombinierter Spanner

Fazit

Quellen

Zeit für Fragen